Quantum Computing with Synthetic Atoms

Trapped ions offer a premiere platform for testing and manipulating isolated quantum systems. Atomic clocks, quantum sensors, and matter-wave interferometry all require exquisite isolation from the decohering effect of their environment. It is by isolating these systems that we finally see nature as it behaves according to the rules of quantum mechanics. It's not that quantum mechanics breaks down for the size and temperature scale of the "everyday world" we know, but rather that the effects of quantum interference become hidden in the noisy thermal average of the commonly experienced universe at human scales.

A particularly vexing problem associated with trapped ion quantum systems (known as "qubits") is that the "easy to use" qubits aren't, well, easy to use. The atomic structure that gives rise to the easiest high-quality qubit comes with the need for difficult laser technology in the ultraviolet. However, this is only really true if we confine ourselves to the species that are found in natural abundance. If we widen the scope to include human-produced isotopes, the ¹³³Ba⁺ ion emerges as the atom that has it all -- an easy to use, robust qubit and optical transitions in the visible part of the spectrum.

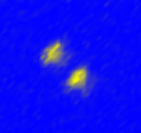
In collaboration with Eric Hudson's group, we have developed methods to produce ¹³³Ba⁺ in our trap and have performed preliminary spectroscopy of its internal structure. The image here shows two ¹³³Ba⁺ ions in the trap ("Dave" is the ion in the upper left, "Justin" is on the lower right), where by exchanging phonons of their collective modes of motion, the hyperfine qubits defined on each atom may be used to perform computations with quantum speed enhancements.

Cold Polar Molecules

The ability to laser cool gas-phase samples of a small subset of elements found in the periodic table has established ultracold atoms as premier systems for precision measurement and control. Select species have been cooled to quantum degeneracy and are finding use as elements in quantum information processors, quantum simulators, and optical atomic clocks. These atoms, however, are extremely symmetric and simple objects when compared to molecules. Even a simple diatomic molecule made from two different elements offers a vast array of new control possibilities if we could only produce and control samples that are as cold and dense as is routinely achieved for atomic samples. It turns out that this is a much more demanding task than it was for atoms, due essentially to the addition of the vibrational degree of freedom that molecules possess.

We are pursuing ways to produce cold samples of polar molecules in the lab. Our focus is on simplicity of both concept and apparatus, and we use a host of different tools to help us, including parts of the electromagnetic spectrum ranging from UV lasers to microwaves to quasi-DC electric fields. As with most atomic physics labs, we also utilize lasers for many tasks, including Q-switched, mode-locked, and continuous-wave lasers. Our plan is to use these tools to decelerate, cool, and trap dense samples of cold molecules for quantum simulation and cold, controlled chemistry.

Atomic Physics in a Beaker

While trapped, gas-phase species can be isolated almost entirely from their environment, their use as sensors can suffer from the fact that there are so few of them. The small number of detections available in a given time introduces what is known as "shot noise" into the measurement result, and if we could perform the same experiments with orders of magnitude more particles, we would. Unfortunately, there is a limit to how densely these species can be packed before they lose their long coherence times, and this limits the achievable signal to noise ratio.

One approach to this trade-off that we are exploring is the use of molecules with atom-like properties that can be dissolved in liquids. Since the density of solutes in liquid can be orders of magnitude higher than gas-phase sensors in use, the potential to lower the shot noise floor makes this attractive.

Along with our collaborators in the Alexandrova, Caram, and Diaconsecu groups in the Department of Chemistry and Biochemistry, we are exploring a molecule that exhibits a narrow optical absorption line when dissolved in a room temperature liquid. Our hope is that by understanding how to engineer soluble molecular armor around optically addressable metal atoms, the coherence of the electrons on the metal can be protected from the effects of the environment.

Qubits and Metastable States

The ground states of trapped atomic ions provide a straightforward place to store quantum information. These hyperfine qubits have long coherence times (~ 1 hour), but can be limiting in laser-driven operations since spontaneously emitted photons tend to scramble their information without warning.

Unlike the other species in use, the ytterbium ion has an excited state whose lifetime is so long that it is effectively another ground state. We are investigating how this F state can be used to augment the quantum toolbox of trapped ion processors with novel measurement capabilities and for extremely high fidelity operation.

Trapped Ion Gyroscope

Imagine you have been tasked with proving to a skeptic that sun does not orbit the Earth, but rather that the Earth is spinning about its axis. No amount of referencing books or papers will convince this person -- they must see it with their own eyes. How can it be done?

Well, if the Earth is spinning, we are spinning along with it and there should be some effects of this motion. And indeed there are, but none seem to be quite as compelling as the precession of a Foucault pendulum. A pendulum, carefully set into motion at any latitude other than the equator, will gradually change its plane of rotation as viewed by an observer rotating with the spinning Earth. Such a device is known as a gyroscope -- a sensor for rotation.

Consider an arrow that always points the same direction in space (say, always toward the same star that is infinitely far away). If we close it up in a box and then open the box later and the arrow seems to point in a different direction, it is the box that has rotated, not the arrow. From this the orientation of the box can be determined, which is a useful navigational tool in situations where GPS is not available.

Along with Paul Hamilton's group, we are creating a gyroscope based on a trapped ion. The rules of quantum mechanics that permit objects to be in two places at once also allow us to make a quantum Foucault pendulum, where the ion orbits the trap center clockwise and counterclockwise at the same time. Matter-wave interference then allows read-out of the orientation of this gyroscope compared to the lab.

If the lab has rotated (hint: it most certainly has!), this effect will be visible in the interference pattern. We are working toward demonstrating this first inertial sensor built from a trapped ion and exploring its usefulness for practical applications. The hope is that robust, inertial navigation will be possible in GPS denied environments such as underwater, in space, or on other planets.

Quantum Simulations with Trapped Ions

Our knowledge of the behavior of quantum many-body systems is currently limited to those that happen to be theoretically or numerically tractable and those that can be studied in detail experimentally. The world, however, exhibits many systems that are too complex for a complete theoretical description, but too large for an efficient numerical simulation on a classical computer or microscopic experimental probing. Such poorly-understood systems include exotic forms of matter such as spin-liquids and some high-temperature superconductors. We would like to understand the behavior of quantum many-body systems better in order to help us to design useful new materials, understand observed but unexplained behavior, and investigate the borderline between quantum mechanical and thermodynamic behavior.

Recently, a new approach called quantum simulation has begun to be applied that is in many ways an ideal intermediate between in situ experiment and numerical simulation. In quantum simulation, we can use a well-controlled, isolated, laboratory quantum system to model the quantum many-body phenomenon of interest. The quantum simulator, then, utilizes the enormous, classically intractable Hilbert space we allow it to fill and, for instance, either does or does not exhibit the superconductivity we were not sure was associated with the Hamiltonian imposed on the simulator. We are using trapped atomic ions as a platform for quantum simulations of a class of many-body quantum systems called lattice spin models. Each ion simulates the quantum-mechanical spin-1/2 degree of freedom of an electron, and by using appropriately tuned laser fields, we can cause these simulated spins to interact in a manner that is governed by the rules we impose on the system. By looking at the resulting spectra, dynamics, phase transitions, and states, we hope to learn about systems that have to this point been inaccessible to us.